1756번: 피자 굽기
첫째 줄에 오븐의 깊이 D와 피자 반죽의 개수 N이 공백을 사이에 두고 주어진다. (1<=D, N<=300,000) 둘째 줄에는 오븐의 최상단부터 시작하여 깊이에 따른 오븐의 지름이 차례대로 주어진다. 셋째 줄
www.acmicpc.net
1. 유형
구현, 이분 탐색, 그리디
2. 자료구조
없음
3. 기능
- 오븐의 지름 재설정
- 재설정 된 오븐에 들어갈 수 있는 반죽 찾기
4. 풀이
구현 문제로 분류 돼있지만 그리디 적인 요소가 더 강한 문제다.
문제를 접근할 때, 오븐의 지름을 재 설정해 줘야한다.

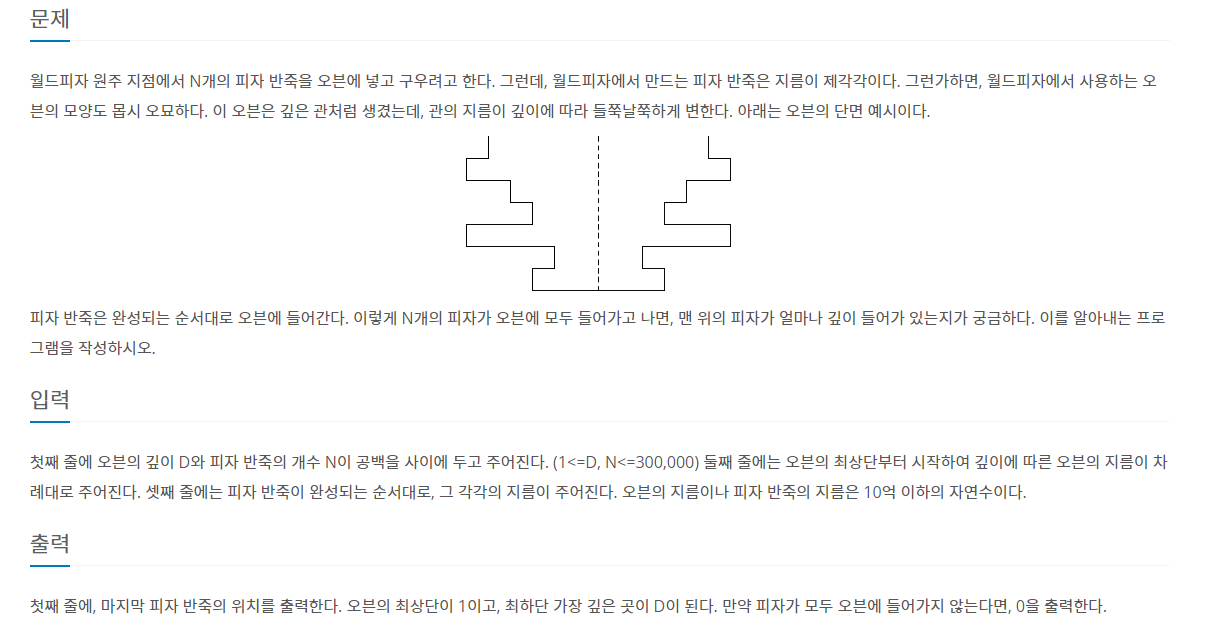
위에 처럼 보라색이 실제로 반죽이 들어갈 수 있는 오븐의 지름이다.
반복문을 통해 재 설정해준다.
위 처럼 만들면 자동으로 정렬이 된 상태이다. 따라서 이분탐색을 진행 해주면 끝.
코트.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int D, N;
static int arr[];
static int dep, min;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine());
D = Integer.valueOf(st.nextToken());
N = Integer.valueOf(st.nextToken());
arr = new int[D];
st = new StringTokenizer(in.readLine());
for (int i = 0; i < D; i++) {
arr[i] = Integer.valueOf(st.nextToken());
}
go();// 지름 재설정
dep = D-1;
min = Integer.MAX_VALUE;
st = new StringTokenizer(in.readLine());
for (int i = 0; i < N; i++) {
int target = Integer.valueOf(st.nextToken());
binary(target, 0, dep );
}
min++;
System.out.println(min);
}
static void go() {
for (int i =1; i<D; i++) {
if(arr[i] > arr[i-1]) {
arr[i] = arr[i-1];
}
}
}
static void binary(int target, int topIdx, int botIdx) {
int res = -1;
while (topIdx <= botIdx) {
int mid = (topIdx + botIdx) / 2;
if (arr[mid] >= target) {
res = mid;
topIdx = mid + 1;
} else {
botIdx = mid - 1;
}
}
min = Math.min(min, res);
dep = res-1;
}
}
최근에 이분탐색에서 파생된 lower bound라는 것을 배웠다. 따라서 이 문제에도 lower bound를 적용할 수 있을거 같아서 다시 풀어봤다. 위의 풀이보다 시간을 더 줄이는 것이 가능했다.
로직)
1. 오름차순 정렬
2. 타깃보다 큰 값중에서 최소값 찾기
코드
import java.util.*;
import java.io.*;
public class Main {
static int arr[];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st =new StringTokenizer(in.readLine());
int D, N;
D = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
st =new StringTokenizer(in.readLine());
arr = new int[D];
for(int i=0; i<D; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
for(int i=1; i<D; i++) {
if( arr[i-1] < arr[i]) {
arr[i] = arr[i-1];
}
}
int low=-1;
int high=D-1;
Arrays.sort(arr);
st =new StringTokenizer(in.readLine());
for(int i=0; i<N; i++) {
int n = Integer.parseInt(st.nextToken());
low=search(++low, high, n);
if(low==-1)
break;
}
if(low==-1)
System.out.println(0);
else
System.out.println(D-low);
}
static int search(int low, int high, int target) {
boolean flag = false;
while(low < high) {
int mid = (low+high)/2;
if(target <= arr[mid]) {
high = mid;
flag=true;
}else {
low = mid+1;
}
}
if(flag)
return high;
else
return -1;
}
}
5. 느낀점
코테에도 이분탐색이 많이 나오는 편이다.
좋은 연습이 됐다.
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 1922 - 네트워크 연결(Java) (0) | 2021.01.07 |
|---|---|
| 백준 18405 - 경쟁적 전염 (0) | 2021.01.05 |
| 백준 9944 - NxM 보드 완주하기 (Java) (0) | 2021.01.04 |
| 백준 18808 - 스티커 붙이기(Java) (0) | 2021.01.04 |
| 백준 17472 - 다리 만들기2 (Java) (0) | 2021.01.03 |
