https://www.acmicpc.net/problem/18223
18223번: 민준이와 마산 그리고 건우
입력의 첫 번째 줄에 정점의 개수 V와 간선의 개수 E, 그리고 건우가 위치한 정점 P가 주어진다. (2 ≤ V ≤ 5,000, 1 ≤ E ≤ 10,000, 1 ≤ P ≤ V) 두 번째 줄부터 E개의 줄에 걸쳐 각 간선의 정보
www.acmicpc.net
유형
다익스트라
문제분석
플로이드 와샬을 쓰려고 했지만 인풋값이 너무 커서 3중 for문에서 시간초과가 날 것입니다.
따라서 최단거리 알고리즘 중 하나인 다익스트라를 사용

설계를 하자면

코딩화
가장 큰 핵심은 다익스트라 구현입니다.
다익스트라의 핵심

미리 구해놓은 경로보다 현재의 새로운 경로가 더 가까울시 갱신.
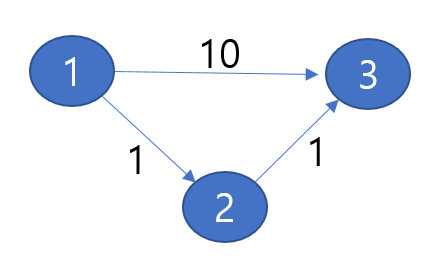
위와 같은 상황, 1->3까지 가는것 보다, 1->2->3을 거치는 것이 더 가깝습니다.
코드
import java.util.*;
import java.io.*;
public class Main {
static List<int[]> list[];
static int INF = 987654321;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine());
int V = stoi(st.nextToken());// 정점수
int E = stoi(st.nextToken());// 간선수
int P = stoi(st.nextToken());// 타깃
list = new ArrayList[V + 1];
for (int i = 1; i < V + 1; i++) {
list[i] = new ArrayList<>();
}
for (int i = 1; i <= E; i++) {
st = new StringTokenizer(in.readLine());
int from = stoi(st.nextToken());
int to = stoi(st.nextToken());
int val = stoi(st.nextToken());
list[from].add(new int[] { to, val });
list[to].add(new int[] { from, val });
}
int len1 = solve(1, P, V) + solve(P, V, V);
int len2 = solve(1, V, V);
if (len1 == len2) {
System.out.println("SAVE HIM");
} else
System.out.println("GOOD BYE");
}
static int solve(int start, int end, int V) {
Queue<int[]> pq = new PriorityQueue<>((a, b) -> (a[1] - b[1]));
boolean visit[] = new boolean[V + 1];
int[] shortest = new int[V + 1];
for (int i = 0; i < V + 1; i++)
shortest[i] = INF;
shortest[start] = 0;
pq.add(new int[] { start, 0 });
while (!pq.isEmpty()) {
int cur[] = pq.poll();
int curnode = cur[0];
if (visit[curnode])
continue;
visit[curnode] = true;
if (curnode == end) {
return shortest[end];
}
for (int[] next : list[cur[0]]) {
int nextedge = next[1];
int nextnode = next[0];
if (!visit[nextnode] && shortest[nextnode] > shortest[curnode] + nextedge) {
shortest[nextnode] = shortest[curnode] + nextedge;
pq.add(new int[] { nextnode, nextedge });
}
}
}
return shortest[end];
}
static int stoi(String s) {
return Integer.valueOf(s);
}
}'알고리즘 > 백준' 카테고리의 다른 글
| 백준 - 1059 (Java)좋은 구간 (0) | 2021.08.19 |
|---|---|
| 백준 16985 - (Java) Maaaaaaaaaze (0) | 2021.08.17 |
| [devmoon]백준 14938 - 서강그라운드 (0) | 2021.07.17 |
| [devmoon]백준 18403 - (Java) 무기공학 (0) | 2021.07.13 |
| [devmoon]백준 15566 - (Java)개구리1 (0) | 2021.07.13 |
